Hi all.Please take up the Electrical Engineering Test-2.Before starting the test take a paper and pen for rough work.Donot use calculator.Questions have been prepared in such a way that you can gain knowledge of some concepts.Some of these questions were asked in competitive exams.Get ready and start the Test !!Your valuable comments are welcome to improve the quality of the tests.
1. If the resistance of a material at 0 ℃ is 3.83 Ω and its temperature co-efficient,∝ =2.27 ×10ˉ3 ℃ˉ1, What is the resistance at 60 ℃
A) 4.15 Ω
B) 4.35 Ω
C) 4.45 Ω
D) 4.20 Ω
ANSWER :
B) 4.35 Ω
EXPLANATION :
Rt = R0(1+∝T) = 3.83(1+(2.27×10ˉ3)*60)
= 3.83(1.1362) = 4.35 Ω.
EXPLANATION :
Rt = R0(1+∝T) = 3.83(1+(2.27×10ˉ3)*60)
= 3.83(1.1362) = 4.35 Ω.
2. Three resistances 7 Ω,8 Ω,10 Ω are connected in series across a 100 V source. What is the current through 10 Ω resistor ?
A) 5 A
B) 20 A
C) 4 A
D) 40 A
ANSWER :
C) 4 A.
EXPLANATION :
Rtotal = 7+8+10 = 25 Ω
Is = Vs/Rtotal = 100 /25 = 4 A
Current is same across all the three resistors as they are connected in series.
EXPLANATION :
Rtotal = 7+8+10 = 25 Ω
Is = Vs/Rtotal = 100 /25 = 4 A
Current is same across all the three resistors as they are connected in series.
3. Three resistances 10 Ω, 8 Ω,4Ω are connected in parallel across 100 V source.Find the power drawn by 8 Ω.
A) 1.25 KW
B) 1150 W
C) 1000 W
D) 1200 W
ANSWER :
A) 1.25 KW
EXPLANATION :
I8Ω = 100/8 = 12.5 A
P8Ω = (I8Ω)^2×R = 12.5×12.5×8 = 1250 W (or) 1.25 KW
P8Ω = V×I8Ω = 100×12.5 = 1250 W (or) 1.25 KW
Voltage is same across all the three resistors as they are connected in parallel.
EXPLANATION :
I8Ω = 100/8 = 12.5 A
P8Ω = (I8Ω)^2×R = 12.5×12.5×8 = 1250 W (or) 1.25 KW
P8Ω = V×I8Ω = 100×12.5 = 1250 W (or) 1.25 KW
Voltage is same across all the three resistors as they are connected in parallel.
4. Find Rab
A) 20 Ω
B) 18 Ω
C) 19 Ω
D) 17 Ω
ANSWER :
C) 19 Ω
EXPLANATION :
1/Rcd = (1/4)+(1/6)+(1/3) = (3+2+4)/12 =9/12
Rcd = 12/9 = 1.33 Ω
1/Rae = (1/(.77+.33+6))+(1/8) = (1/8)+(1/8) = 2/8
Rae = 8/2 = 4 Ω
Rab = 4+15 = 19 Ω
EXPLANATION :
1/Rcd = (1/4)+(1/6)+(1/3) = (3+2+4)/12 =9/12
Rcd = 12/9 = 1.33 Ω
1/Rae = (1/(.77+.33+6))+(1/8) = (1/8)+(1/8) = 2/8
Rae = 8/2 = 4 Ω
Rab = 4+15 = 19 Ω
5. Determine magnitude & direction of I
A) 9A into the node
B) 8A awaythe node
C) 9A awaythe node
D) 8A into the node
ANSWER :
D) 8A into the node
EXPLANATION :
Assume inward direction as positive.
I-2+6+5-3-7+1-3 = 0
I = 8A
direction is into the node.
EXPLANATION :
Assume inward direction as positive.
I-2+6+5-3-7+1-3 = 0
I = 8A
direction is into the node.
6. Two resistances R1 = 10 Ω & R2 = 30 Ω are connected in parallel and are supplied by a current sourcw I = 5 A. Find the power consumed by 10 Ω.
A) 130.525 Watts
B) 145.625 Watts
C) 140.625 Watts
D) 150 Watts
ANSWER :
C) 140.625 Watts
EXPLANATION :
P10Ω =
(I10Ω)^2×R1 = [(I×R2)/(R1+R2)]^2×R1
= [(5×5×30×30)/(40×40)]×10 = (25×900)/(4×40)
= 5625/40 = 140.625 Watts
EXPLANATION :
P10Ω =
(I10Ω)^2×R1 = [(I×R2)/(R1+R2)]^2×R1
= [(5×5×30×30)/(40×40)]×10 = (25×900)/(4×40)
= 5625/40 = 140.625 Watts
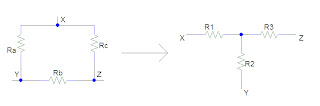
7. Ra = 5 Ω , Rb = 8 Ω , Rc = 7 Ω , R2 = ?
A) 4 Ω
B) 3 Ω
C) 2 Ω
D) 1.5 Ω
ANSWER :
C) 2 Ω
EXPLANATION :
R2 = (RaRb)/(Ra+Rb+Rc)
= (5×8)/(5+8+7) = 40/20 = 2 Ω
EXPLANATION :
R2 = (RaRb)/(Ra+Rb+Rc)
= (5×8)/(5+8+7) = 40/20 = 2 Ω
8. Find Rth
A) 55 Ω
B) 50 Ω
C) 65 Ω
D) 60 Ω
ANSWER :
D) 60 Ω
EXPLANATION :
To find the Thevenin's Resistance short circuit the voltage source
Rth = [1/((2+3)/60)]+48 = [60/5]+48 = 12+48 = 60 Ω
EXPLANATION :
To find the Thevenin's Resistance short circuit the voltage source
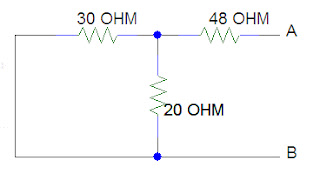
9. The value of R required for maximum power transfer in the network
A) 2 Ω
B) 4 Ω
C) 8 Ω
D) 16 Ω
ANSWER :
C) 8 Ω.
EXPLANATION :
To find the Thevenin's Resistance short circuit the voltage source,open circuit the current source and the load resistance.
For maximum power transfer RL = Rth
Rth = [(20×5)/(20+5)]+4 = [100/25]+4 =4+4 = 8 Ω
EXPLANATION :
To find the Thevenin's Resistance short circuit the voltage source,open circuit the current source and the load resistance.
For maximum power transfer RL = Rth
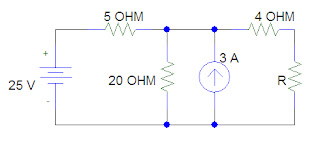
10. The current Source given in the figure can be represented by equivalent voltage source of
A) 20V with 4Ω in series
B) 20V with 4Ω in parallel
C) 5V with 4Ω in series
D) 5V with 4Ω in parallel
ANSWER :
A) 20V with 4Ω in series
No comments:
Post a Comment